La distribución Geométrica o de Pascal
Algunas puntualizaciones de la
definición de X:
- Nótese que, en esta definición, condiciones independientes significa
que p, la probabilidad de A, y 1 − p,
la de su complementario Ac, no varían a
lo largo de las sucesivas repeticiones de la experiencia.
- Tal y como la hemos definido, X se refiere al número de lanzamientos hasta que se produce A, pero sin contabilizar el último caso en que se da A. Por dicha razón X puede tomar los valores k = 0, 1, 2, ... con probabilidad no nula.
Un ejemplo de este modelo podría ser la
experiencia consistente en lanzar sucesivamente un dado regular hasta que
aparezca el número 6. Si definimos la variable aleatoria X como
el número de lanzamientos de un dado regular hasta que aparezca un 6,
queda claro que X sigue una distribución geométrica de
parámetro p = 1/6.
Preguntas:
- ¿A qué suceso nos referimos cuando decimos X = 0?
Solución
|
Cuando decimos que X =
0 nos referimos al caso en que el 6 aparece en el primer lanzamiento. La
probabilidad de que esto suceda, suponiendo un dado regular, es de 1/6:
P[X = 0] = 1/6
|
- ¿Cuál es la probabilidad de que el primer 6 aparezca en el cuarto
lanzamiento?
Solución
La probabilidad de que el primer 6 aparezca en el cuarto lanzamiento
corresponde a:
P[X = 3] = (5/6)3 ´ 1/6
= 0,0965
Fijémonos en que, si definimos A como el suceso sale
un 6, la probabilidad anterior corresponde a la del suceso: {Ac Ac Ac A} (en
este orden).
Propiedades del modelo Geométrico o dePascal
1) Esperanza: E(X) =
(1 − p)/p
2) Varianza: V(X) =
(1 − p)/p2

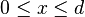


 .
.



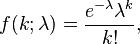
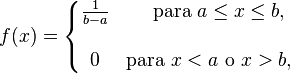
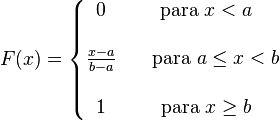

 para toda
para toda 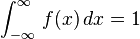




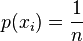
![F(x)=\frac{1}{n} \sum_i 1_{(-\infty,x]}(x_i)\,\!.](http://upload.wikimedia.org/math/d/1/9/d19f430201b6527b7e1205811c266aea.png)


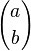
![E[X]=\frac{nd}{N}](http://upload.wikimedia.org/math/e/d/b/edb7931c237719680795389c71e2ca37.png)
![Var[X]=\bigg(\frac{N-n}{N-1}\bigg)\bigg(\frac{nd}{N}\bigg)\bigg( 1-\frac{d}{N}\bigg).](http://upload.wikimedia.org/math/9/b/2/9b21150dd51ee2e8e3c219b9d6c67cdd.png)


![Var[X]=npq\frac{N-n}{N-1}.](http://upload.wikimedia.org/math/8/4/5/8450776365971ac3ed36f95d91b68b22.png)