La distribución de probabilidad de una variable aleatoria continua X está caracterizada por una función f(x) que recibe el nombre de función de densidad de probabilidad. Esta función f(x) no es la misma función de probabilidad de una variable aleatoria discreta.
La gráfica de la función f(x) es una curva que se obtiene para un número muy grande de observaciones y para una amplitud de intervalo muy pequeña.
Esta función de densidad de probabilidad f(x) permite calcular el área bajo la curva que representa la probabilidad de que la variable aleatoria continua X tome un valor entre el intervalo donde se define la función.
De las propiedades de la función de distribución se siguen las siguientes propiedades:
 para toda x.
para toda x.- El área total encerrada bajo la curva es igual a 1:
- La probabilidad de que X tome un valor en el intervalo [a,b] es el área bajo la curva de la función de densidad en ese intervalo o lo que es lo mismo, la integral definida en dicho intervalo. La gráfica f(x) se conoce a veces como curva de densidad.
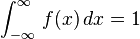

No hay comentarios:
Publicar un comentario