viernes, diciembre 07, 2012

DISTRIBUCIÓN HIPERGEOMÉTRICA

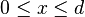
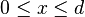
La distribución hipergeométrica es una distribución discreta relacionada con muestreos aleatorios y sin reemplazo. Supóngase que se tiene una población de N elementos de los cuales, d pertenecen a la categoría A y N-d a la B. La distribución hipergeométrica mide la probabilidad de obtener x  0 \le x \le d elementos de la categoría A en una muestra de n elementos de la población original.
Puede deducirse a través de razonamientos combinatorios y es igual a
P(X=x)=\frac{{d \choose x}{{N-d \choose n-x}}}{{N \choose n}},
Donde N es el tamaño de población, n es el tamaño de la muestra extraída, d es el número de elementos en la población original que pertenecen a la categoría deseada y x es el número de elementos en la muestra que pertenecen a dicha categoría.
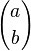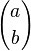La notación {a \choose b} hace referencia al coeficiente binomial, es decir, el número de combinaciones posibles al seleccionar b elementos de un total a.

El valor esperado de una variable aleatoria X que sigue la distribución hipergeométrica es
E[X]=\frac{nd}{N}
y su varianza,
Var[X]=\bigg(\frac{N-n}{N-1}\bigg)\bigg(\frac{nd}{N}\bigg)\bigg( 1-\frac{d}{N}\bigg).
En la fórmula anterior, definiendo
p = \frac{d}{N}
y
q = 1-p\,,
se obtiene
Var[X]=npq\frac{N-n}{N-1}.
La distribución hipergeométrica es aplicable a muestreos sin reemplazo y la binomial a muestreos con reemplazo. En situaciones en las que el número esperado de repeticiones en el muestreo es presumiblemente bajo, puede aproximarse la primera por la segunda. Esto es así cuando N es grande y el tamaño relativo de la muestra extraída, n/N, es pequeño.
Publicado por MARCOS HINOJOSA HERNANDEZ en viernes, diciembre 07, 2012

1 comentario:

  1. Unknown13 de diciembre de 2012, 14:12

    Profesor Marcos, ha tratado Usted un tema complejo pero fundamental, me parece que seria mucho mas compresible para los estudiantes a través de la aplicación de los conceptos a situaciones de la vida cotidiana.

    Cecilia Galvis

    ResponderEliminar

Suscribirse a: Enviar comentarios (Atom)